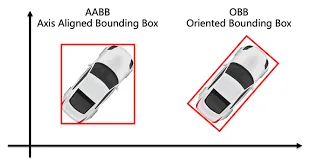
上一篇文章说到了,基于包围形的方法是一种粗略的碰撞检测方法,基于外接圆形的方法运算速度很快,但精度很差;基于轴对齐包围盒(AABB)的方法适合本身就是矩形的物体,其运算速度非常快,但检测精度还是不够。
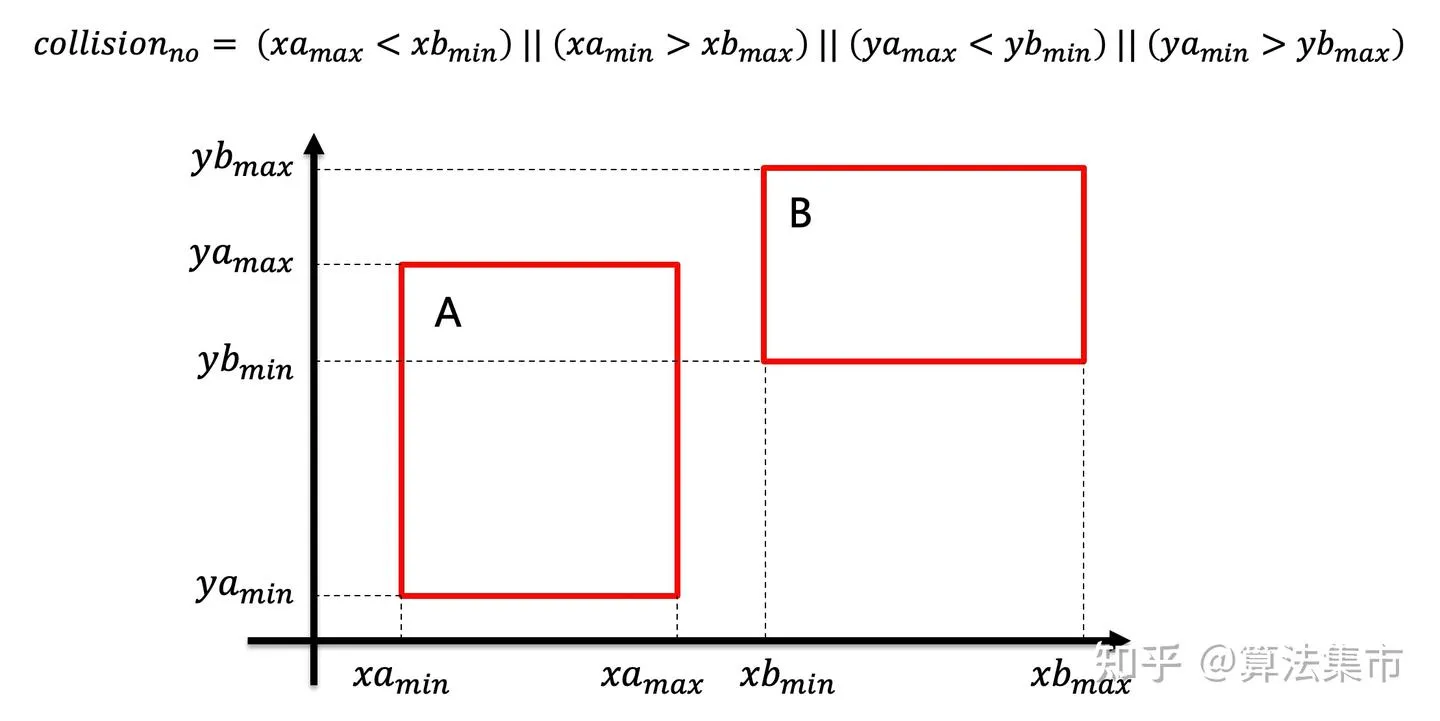
所以接下来我们来说说OBB和SAT。
OBB
OBB 检测,即有向包围盒(Oriented Bounding Box)检测,是一种检测两个物体有没有相交的算法。物体根据包围盒中心、包围盒大小以及包围盒旋转轴构造有向包围盒,该包围盒比 AABB包围盒更贴合旋转物体。OBB 检测利用 SAT(Separating AxisTheorem)分离轴算法进行相交检测,比 AABB检测具有更好的检测精度。
SAT算法原理
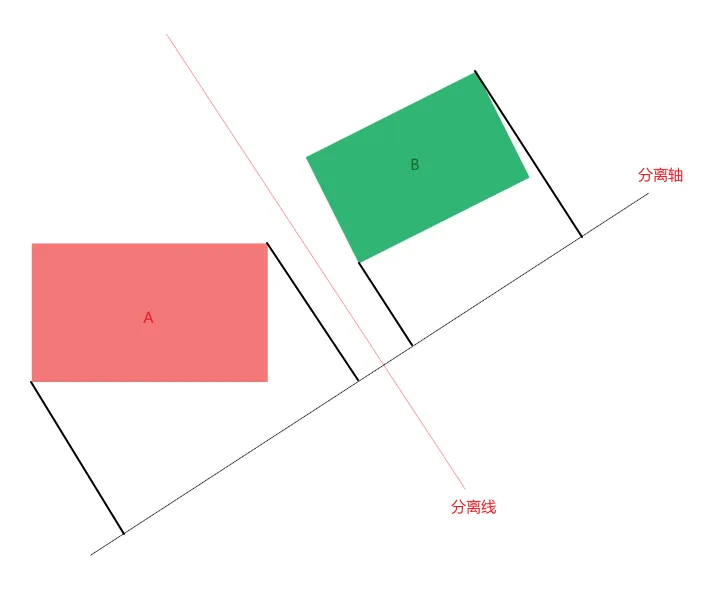
对于两个凸多边形来说,若存在一条直线把两个凸多边形分开,那么垂直于这条直线的轴则称为分离轴。若两个物体在分离轴上的投影不相交,则两个物体不相交,并且一旦在某个轴上存在不相交的情况,则两个物体一定不相交,退出检测。
在实际运用中,我们常以凸多边形的边的垂线作为分离轴,依次检测物体在分离轴上的投影。
2维
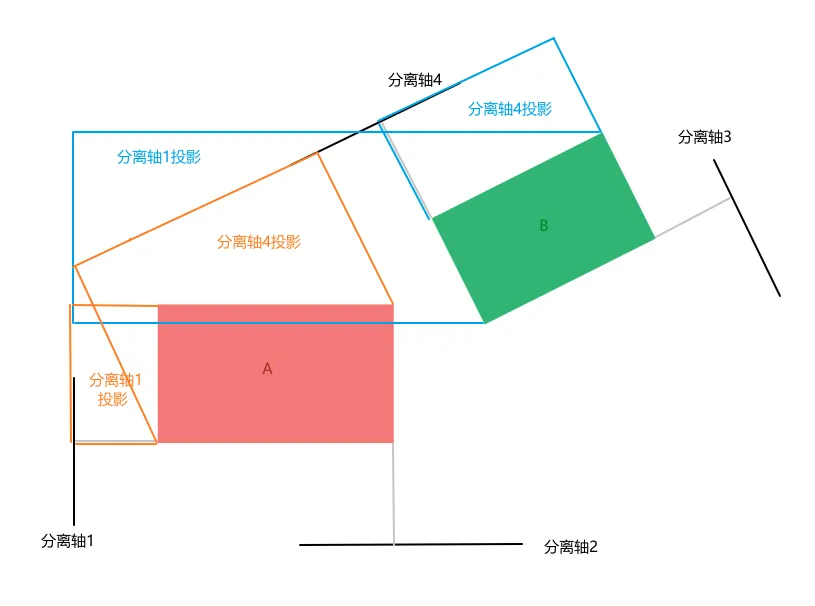
在 2D 图形中,分离轴的数量为两个凸多边形物体的边数之和,如上图所示,4 条黑色的轴为分离轴。在分离轴 1 上,我们观察到物体 A的投影和物体 B 的投影相交了,因此在分离轴 1 上,两个物体相交;在分离轴 2 上,我们观察到两个物体的投影没有相交,因此两个物体在分离轴 2 上没有相交。
由此,我们可以得出 A、B 两个物体没有相交。通过观察图像我们也知道这个结果没错。
实操
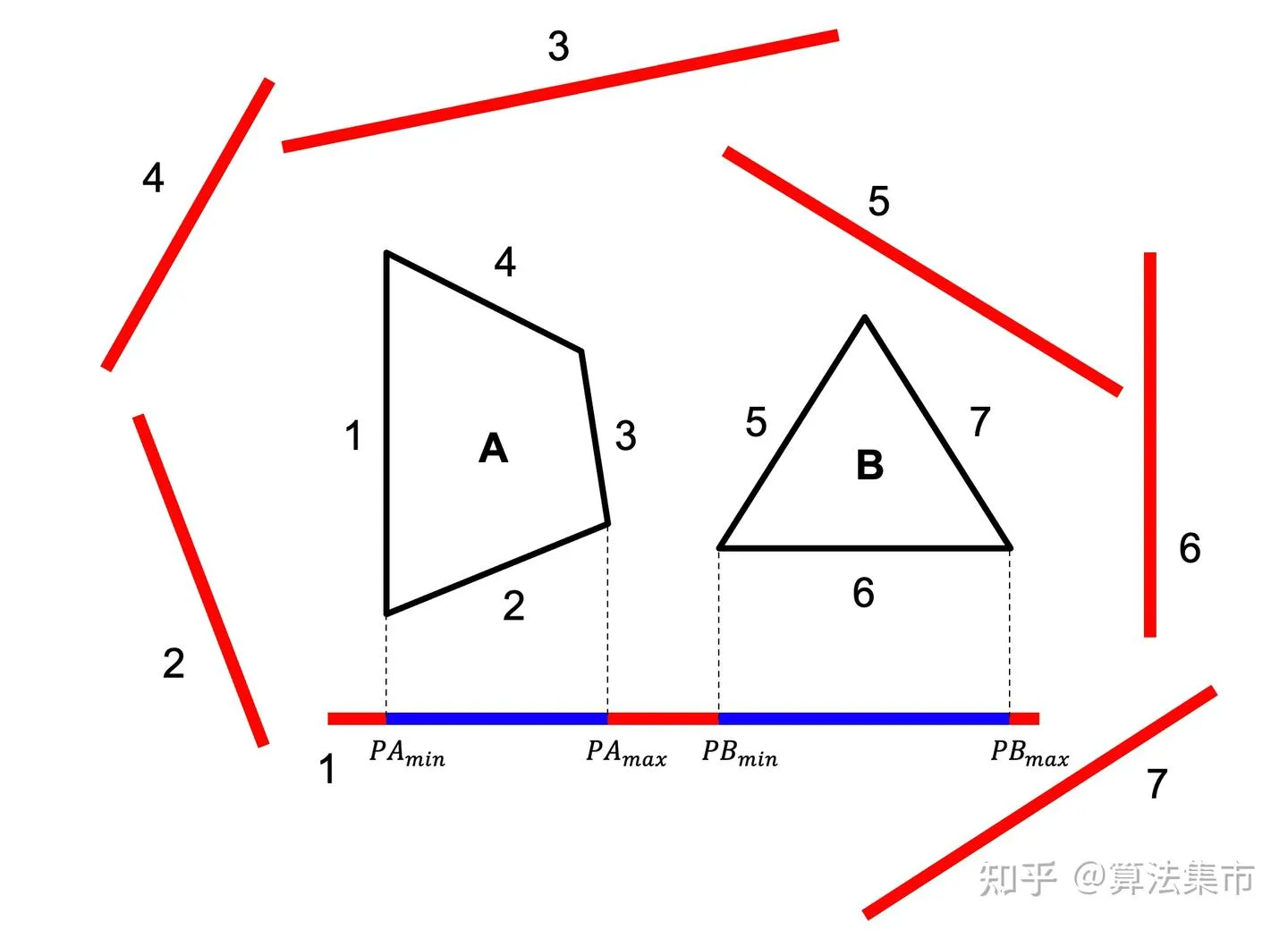
以下图中的两个多边形 A 和 B 为例,分离轴定理的具体步骤为:
- 首先根据边1的两个顶点位置坐标,计算出边1的向量,设为(x,y);
- 进而求出边1的法向量,作为分离轴,为(y, -x)或(-y,x)。若需要求两个多边形的最小分离距离,这里的法向量还需要化为单位向量;若只需判断两个多边形是否相交,则不需要化为单位向量;
- 依次将多边形 A 和 B 的所有顶点与原点组成的向量投影到这个分离轴上,并记录两个多边形顶点投影到分离轴上的最小值和最大值(Pmin,Pmax),形成一个投影线段;
- 判断这两个投影线段是否发生重叠,若不重叠,则有 (PAmax < PBmin)||(PAmin > PBmax);
- 若两个投影线段不重叠,则代表存在这样一条直线将两个多边形分开,两个多边形不相交,可以直接退出循环;
- 若两个投影线段重叠,则回到步骤1,继续以边2的法向量作为分离轴,进行投影计算;
- 当两个多边形的所有边都检查完之后,找不到这样一条分离的直线,则意味着两个多边形相交。
3维
在 3D 中,我们以一个有向的长方体来包围物体,即 OBB。
由于长方体的坐标轴两两垂直,因此坐标轴即是分离轴。由于两个长方体之间还存在特殊的摆放。

在这种情况下,两个包围盒的坐标轴分离轴投影均相交,但是这两个物体并没有相交,两个物体之间还是存在一个面能够把两个物体分开,这个面就是向量 A 和向量 B 构成的平面。
利用向量叉乘的性质,我们可以求出一个垂直于这个面的向量,我们以这个向量为新的分离轴。两个物体每两条边构成的面都需要求垂直向量,因此两个 OBB 包围盒之间有 3 * 3 = 9 条新的分离轴。加上原来两个向量的 3 + 3 = 6 条分离轴,在 3D 中一共要检测 15条分离轴。
对于其中一条分离轴,我们遍历顶点作为向量,投影到分离轴上,筛选出最大和最小值。对两个物体进行同样的操作后,我们比较两个物体的投影最值有无相交。每条分离轴以此方法操作即可。
//包围盒数据结构
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class CollisionData : MonoBehaviour
{
public Vector3[] vertexts = new Vector3[8];
public Vector3[] axes = new Vector3[3];
public Vector3 center = Vector3.zero;
}
---------------------------------------------
/// <summary>
/// SAT分离轴碰撞检测之OBB检测
/// <param name="data1"></param>
/// <param name="data2"></param>
/// </summary>
private bool CollisionOBB(CollisionData data1,CollisionData data2)
{
//求与两个OBB包围盒之间两两坐标轴垂直的法线轴 共9个
int len1 = data1.axes.Length;
int len2 = data2.axes.Length;
Vector3[] axes = new Vector3[len1 + len2 + len1 * len2];
int k = 0;
int initJ = len2;
for (int i = 0; i < len1; i++)
{
axes[k++] = data1.axes[i];
for (int j = 0; j < len2; j++)
{
if (initJ > 0)
{
initJ--;
axes[k++] = data2.axes[j];
}
axes[k++] = Vector3.Cross(data1.axes[i], data2.axes[j]);
}
}
for (int i = 0, len = axes.Length; i < len; i++)
{
if (NotInteractiveOBB(data1.vertexts, data2.vertexts, axes[i]))
{
//有一个不相交就退出
return false;
}
}
return true;
}
/// <summary>
/// 计算投影是否不相交
/// </summary>
/// <param name="vertexs1"></param>
/// <param name="vertexs2"></param>
/// <param name="axis"></param>
/// <returns></returns>
private bool NotInteractiveOBB(Vector3[] vertexs1, Vector3[] vertexs2, Vector3 axis)
{
//计算OBB包围盒在分离轴上的投影极限值
float[] limit1 = GetProjectionLimit(vertexs1, axis);
float[] limit2 = GetProjectionLimit(vertexs2, axis);
//两个包围盒极限值不相交,则不碰撞
return limit1[0] > limit2[1] || limit2[0] > limit1[1];
}
/// <summary>
/// 计算顶点投影极限值
/// </summary>
/// <param name="vertexts"></param>
/// <param name="axis"></param>
/// <returns></returns>
private float[] GetProjectionLimit(Vector3[] vertexts, Vector3 axis)
{
float[] result = new float[2] { float.MaxValue, float.MinValue };
for (int i = 0, len = vertexts.Length; i < len; i++)
{
Vector3 vertext = vertexts[i];
float dot = Vector3.Dot(vertext, axis);
result[0] = Mathf.Min(dot, result[0]);
result[1] = Mathf.Max(dot, result[1]);
}
return result;
}
综上,分离轴定理是一种适用于 bounding box 和 polygon 的精细碰撞检测算法,其优点是算法原理简单,可准确判断两个多边形是否相交;缺点在于当多边形的边数较多时,该算法的效率较低(当两个多边形相交时,需要遍历完所有边进行判断)。
在实际应用中,为了提高效率,通常 先使用 基于轴对齐包围矩形(AABB)的方法进行粗略的碰撞检测,然后再使用 分离轴定理(SAT)做精细碰撞检测 。
同时值得一提的是,OBB 检测只能是凸多边形,不适用于凹多边形的情况。凹多边形可以分割为凸多边形进行检测。