Motivation
球谐函数(Spherical Hamonics, SH)在图形学主要应用在实时渲染和光照(Realtime Rendering & Lighting)领域。
它主要用来高效地表示和处理球面上的数据,比如光照、反射、阴影等。
最著名的一个应用是游戏引擎中的光照探针(Lighting Probe),光照探针用于捕获和模拟场景中的光照信息。具体来说,光照探针是一个虚拟的采样点,放置在三维场景中的某个位置,用来记录从该点向周围环境辐射的光照数据。这些数据包括光的方向、强度、颜色等信息,通常以球谐函数(Spherical Harmonics)或其他压缩形式存储。光照探针的目的是在不进行完整的光线追踪计算的情况下,为场景中的物体提供近似但逼真的光照效果。
为什么要用球谐函数来存储呢?
我们来看一段相关介绍:

球谐函数的标准正交性,一方面让它可以表示近乎所有的光照信息,另一方面提供了快速的计算查找能力。
而球谐函数的旋转不变性,天然地提供了在3D场景中的高效存读能力,通过很小的算力需求来支撑强大的实时功能。
球谐函数
对于场景中信息的存读,使用文件IO肯定是不现实的,而从内存/GPU中加载,对于设备有较高的要求。但是如果类似深度学习,把信息压缩成一个函数,通过输入的变量来查找呢?
球谐函数就像一套工具,能把这些复杂的信息拆成简单的小块,然后再拼回去。
用一个比喻来解释
假设你在一个房间里,房间里有很多灯,灯光从四面八方照过来,亮度还不均匀。你想告诉朋友这个房间的光是怎么分布的,但直接说“东边有点亮,西边很暗,南边超亮”会很啰嗦。球谐函数就像一套“魔法拼图”:
- 它先把房间里的光照拆成几个基本图案(比如“整体亮度”“东西方向的差别”“南北方向的差别”)。
- 每个图案都有个“强度值”,告诉你这个图案占多大比重。
- 把这些图案加起来,就能差不多还原整个房间的光照分布。
这些基本图案就是球谐函数的基础,它们是一组数学公式,专门用来描述球面上的变化。
在计算机图形学中的应用
在光照探针里,球谐函数特别有用。光照探针采集周围的光照信息(从各个方向来的光),然后用球谐函数把这些信息“压缩”成几个数字(系数)。
渲染的时候,引擎拿着这些系数一算,就能快速知道某个点应该有多亮、什么颜色,而不用每次都重新算所有光线。
- 一方面,球谐函数只要几个系数,就能大致描述出来360度方向的光照,优化了效率
- 一方面,球谐函数通过球面存取数据,擅长处理平滑的变化,比如天空从蓝到橙的渐变,不会显得生硬。
然而,如果光照变化特别复杂(比如有很多小光斑或尖锐阴影),球谐函数可能会“模糊”细节,因为它更适合平滑的大范围光照。所以球谐函数也不是万能的。
除了光照探针,球谐函数还被用于预计算辐射传输(Precomputed Radiance Transfer,PRT),用于处理物体之间复杂的间接光照(比如墙反射的光照到地板上)。
球谐函数的数学原理
数学原理确实有点复杂…
这里给出两篇不错的博客,从应用和理解的角度来分析一下数学原理。
前置数学知识
1.基函数
基函数是函数空间中的基本元素,就像欧几里得空间中的坐标轴一样。任何函数都可以表示为基函数的线性组合。
例如,对于二次多项式空间,可以用基函数组{1,t,t^2}进行线性组合得到,即a+bt+ct^2 。这里{a , b , c}即表示各个基函数的系数。
这种概念类似于二维欧几里得空间中的基向量,但函数空间通常是无限维的,因此需要无限个基函数来完全描述连续函数。
2.谐函数
“谐函数”在数学和物理学中通常指的是满足某些特定条件的函数,尤其是在函数空间(Function Space)或调和分析的背景下。
在数学中,谐函数(Harmonic Function)通常是指满足拉普拉斯方程(Laplace’s Equation)的函数,显著的特征是在二维或三维的欧几里得空间中,函数的二阶偏导数之和为零。
在物理学中,谐函数广泛应用于描述稳态的物理场,如电场(电势)、重力场和流体中的势场。
说明
球谐函数是将谐函数限制在球坐标系下的单位球面的一组基函数。它们可以用来近似球面上的任何函数f(t)。
用数学语言来描述如下:
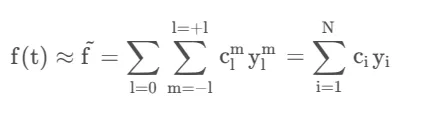
其中,N表示了系数或者说基底函数的数量,理论上需要无限个基函数才能完全恢复连续函数,但在实际中通常只取前几阶(如 l=0,1,2)来近似。
y_1^m被称为球谐基,c_1^m是对应球谐基方向上的系数。
球面空间上的球谐函数y_1^m可视化如下:
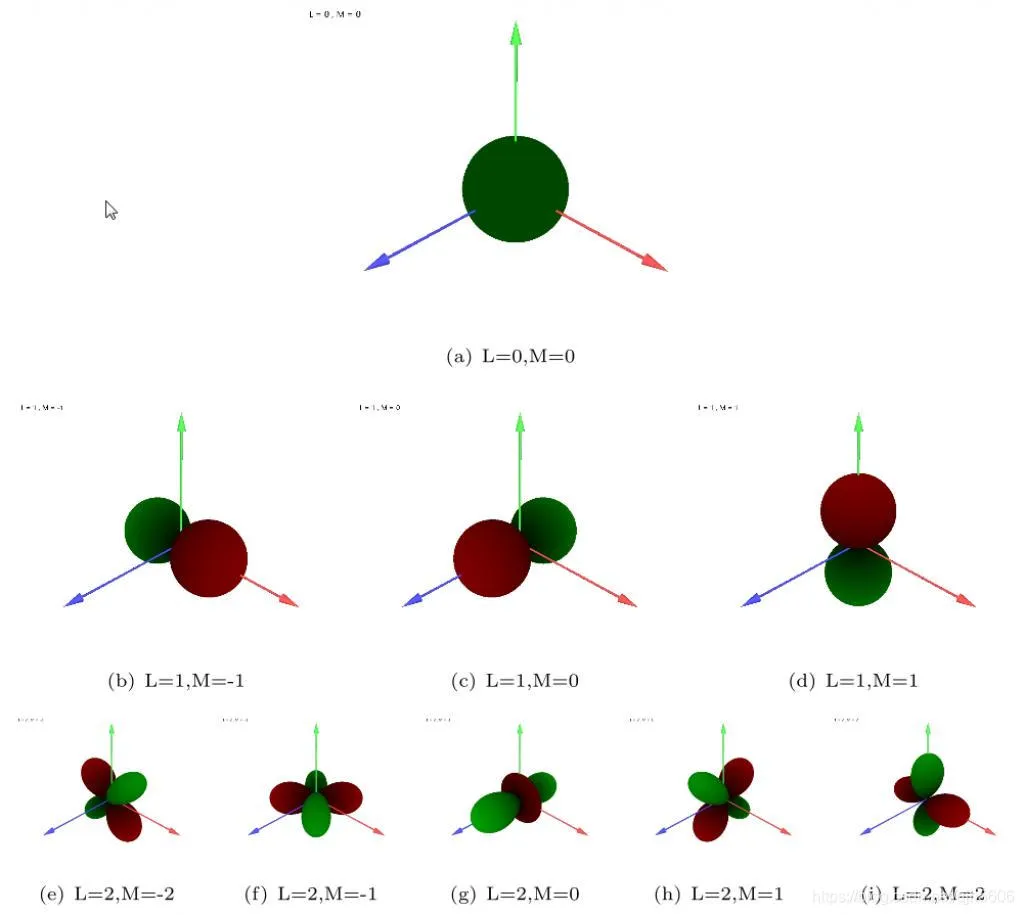
具体的函数表达式可以在这里查看,应用的时候一般不超过3阶。
上图中,绿色表示球谐函数的值为正值,而红色表示球谐函数的值为负值;矢径越大球谐函数值的绝对值越大,反之矢径越小球谐函数值的绝对值越小。
- l=0,m=0时,是一个常数函数,相当于整个球面上的值相同。
- l=1时,对应m=-1,0,1,呈现出类似偶极子的图案,绿色表示正值,红色表示负值,矢径大小反映绝对值的强弱。
- l=2时,对应m=-2,-1,0,1,2,呈现更复杂的象限状图案,反映了更高阶的角动量状态。
在实际的使用中,一般只取前几阶的球谐函数来近似球面上的函数。例如在量子力学中,原子轨道的形状(如 s 轨道为球对称,p 轨道为哑铃状,d 轨道为更复杂的四叶草状)直接对应于低阶球谐函数。而在图形学中,更常用的是球谐函数的实数形式,这一点不同于量子力学的复数形式。
下面给出的是实数形式:

至于投影与重建部分,限于笔者的技术水平,在此就不乱说明了。

