今天我们接着来说说GPU的几何阶段。
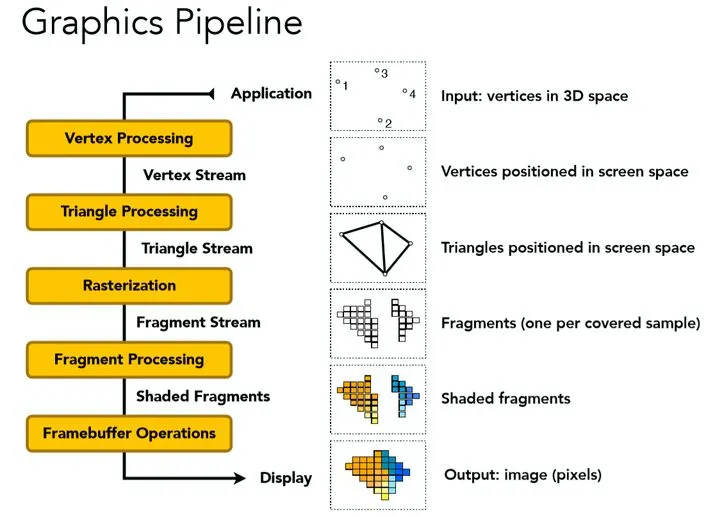
GPU渲染管线由许多步骤组成,比如 顶点处理 、 图元装配及光栅化 、 片元处理 、输出合并等。
GPU阶段(几何阶段部分)
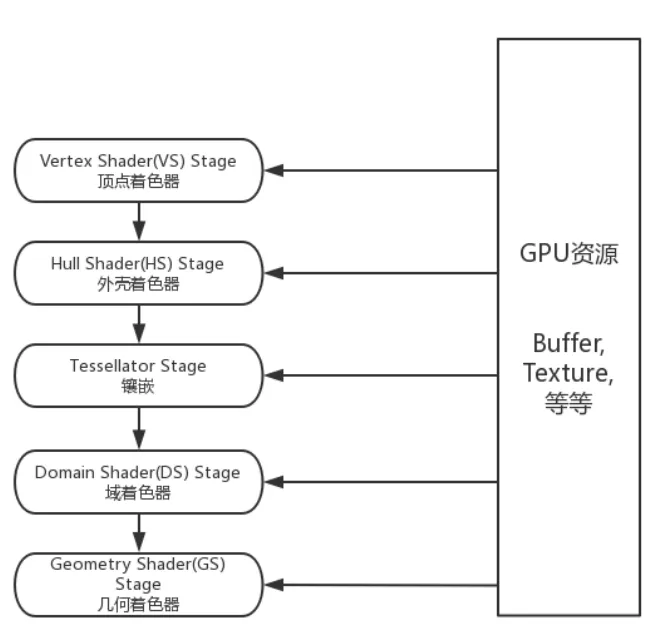
几何阶段在GPU上运行,它处理应用阶段发送的渲染图元,负责大部分的逐三角性和逐顶点操作。几何阶段的一个重要任务就是把顶点坐标变换到屏幕空间中 ,再交给光栅器进行处理。通过对输入的渲染图元进行多步处理后,这一阶段将会输出屏幕空间的二维顶点坐标、每个顶点对应的深度值、着色等相关信息,并传递给光栅化阶段。
几何阶段可以细分为4个子阶段: 顶点着色阶段(Vertex Shading) , 投影阶段(Projection) , 裁剪阶段(Clipping) 和 屏幕映射阶段(Screen Mapping) 。

我们不会按照阶段来介绍,而是顺着阶段,把每一块都理清。
顶点处理
顶点着色器(Vertex Shader)
顶点着色器的处理单位是顶点,也就是说,输入进来的 每个顶点都会调用一次顶点着色器 。它主要执行坐标转换和逐顶点着色的任务。
坐标转换是将顶点坐标从模型空间转换到齐次裁剪空间中 ,它是通过MVP(Model、View、Projection)转换得到的。
·Model 矩阵 : 用于施加世界变换,将一个“快递盒子”里的模型拿出来,摆到场景中。
·View 矩阵:处于对裁剪的考虑,将整个世界进行移动(所以才要对每个顶点施加变换),永远保证相机/观察视口位于原点。
·Projection 矩阵:一般我们会使用类似绘画创作的透视作图来渲染一幅画面,Projection矩阵用于将整个相机录入的空间(视图空间)“拍”到相机的一个二维平面上(正交投影)。但是为了考虑透视,我们的整个观察的区间并不是四棱柱,而是一个类似棱台的形状,此时需要把较远的一段压扁,变成一个四棱柱,再“拍”到二维上(透视投影)。
咱们先来看看理论:
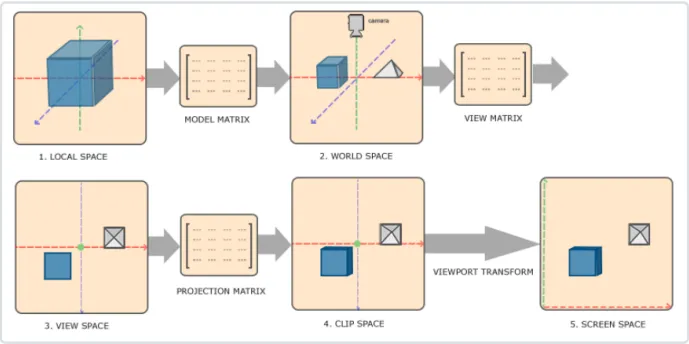
我们从建模工具得到的是物体的局部坐标(Local Coordinate),就好像把手办装到一个快递盒子;局部坐标通过模型矩阵Model变换到世界坐标(World Coordinate),把手办从盒子里拿出来,摆放到场景中;世界坐标通过观察矩阵View变换到观察坐标(View Coordinate);观察坐标经过投影矩阵Projection变换到裁剪坐标(Clip Coordinate);裁剪坐标经过透射除法(Perspective Division)得到标准设备空间(Normalized Device Coordinates,NDC);NDC坐标通过视口变换(Viewport Transformation)变换到窗口坐标进行显示。
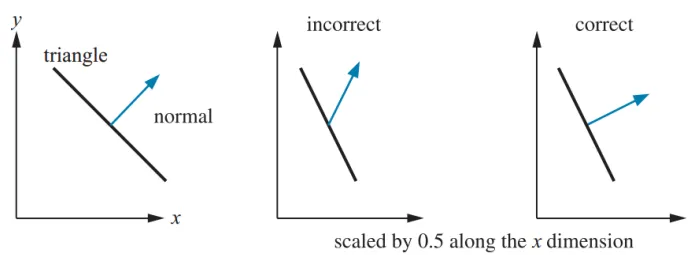
光照计算一般都是在世界空间进行的,所以输入的顶点坐标需要通过乘以模型矩阵变换到世界空间。如果物体变换有非均匀缩放,那么在变换法线时就要注意了。我们不能简单的通过乘以模型矩阵来将法线变换到世界空间。下图展示了法线变换可能产生的问题。如果只是存在平移变换(Translation)我们无需对法线进行变换;如果只存在平移和旋转变换(Rotation)我们只需要乘上渲染矩阵;如果存在非均匀缩放变换(Scaling)我们需要使用矩阵的逆的转置来变换法线。关于该过程的推导可以参考OpenGL Normal VectorTransformation这篇文章。
虚拟摄像机定义了我们的观察空间。世界空间和观察空间的关系如下所示,虚拟摄像机的位置是坐标的原点,观察方向沿着Z轴的负方向。我们可以通过摄像机的位置EyePosition、观察目标点FocusPosition和向上的方向向量UpDirection来构建观察矩阵。OpenGL和DIrectX都有对应的API。该方法的实现比较简单,只需要通过两次向量的叉乘就可以构建该矩阵。
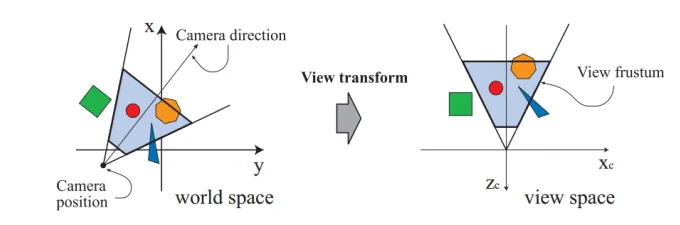
介绍裁剪空间之前,我们需要先来看一个重要的概念:视椎体(Frustum)。视椎体可以通过 上下左右远近六个平面来定义。我们通过投影矩阵将物体从观察空间变换到裁剪空间,裁 剪空间是一个以原点为中心的立方体,不在该裁剪空间的图元都会被裁剪。根据投影方式 的不一样,我们可以定义不同的投影矩阵,常见的投影方法有:正交投影和透视投影。两 种不同投影对应的视椎体如下图所示。我们可以看到正交投影的视椎体是长方体,而透视 投影的视椎体是台体。我们可以通过近平面(Near)、远平面(Far)、垂直视场角(Vertical Field of View, FOV)和屏幕纵横比(Aspect Ratio,也叫作屏幕宽高比)四个参数来定义视 椎体。
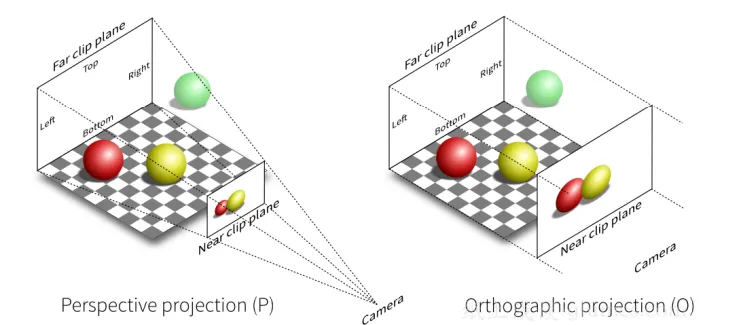
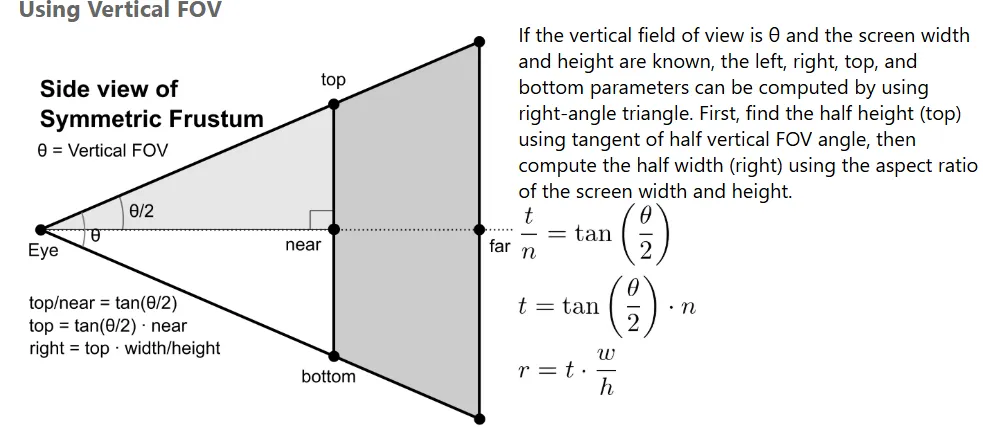
视椎体参数可以这样计算:
当然,代码是少不了的:
// View 矩阵构造
Eigen::Matrix4f get_view_matrix(Eigen::Vector3f eye_pos)
{
Eigen::Matrix4f view = Eigen::Matrix4f::Identity();
Eigen::Matrix4f translate;
translate << 1, 0, 0, -eye_pos[0], 0, 1, 0, -eye_pos[1], 0, 0, 1,
-eye_pos[2], 0, 0, 0, 1;
view = translate * view;
return view;
}
// model矩阵构造
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
float angle = rotation_angle * MY_PI / 180.0f;
Eigen::Matrix4f rotation;
rotation << cos(angle), -sin(angle), 0, 0,
sin(angle), cos(angle), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
model = rotation * model;
return model;
}
// projection 矩阵构造(透视变换)
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
Eigen::Matrix4f persp_to_ortho, ortho_scale, ortho_translate;
float t = tan(eye_fov / 2.0f * MY_PI / 180.0f) * zNear;
float r = t * aspect_ratio;
float l = -r;
float b = -t;
float n = zNear;
float f = zFar;
// 透视空间压缩到正交空间
persp_to_ortho << n, 0, 0, 0,
0, n, 0, 0,
0, 0, f + n, -f * n,
0, 0, 1, 0;
// 正交变换放缩到[-1,1]的裁剪空间
ortho_scale << 2 / (r - l), 0, 0, 0,
0, 2 / (t - b), 0, 0,
0, 0, 2 / (n - f), 0,
0, 0, 0, 1;
// 正交变换Cube移到原点
ortho_translate << 1, 0, 0, -(r + l) / 2,
0, 1, 0, -(t + b) / 2,
0, 0, 1, -(n + f) / 2,
0, 0, 0, 1;
projection = ortho_scale * ortho_translate * persp_to_ortho * projection;
return projection;
}看不懂数学公式?没关系,接下来我会给出解释。
正交投影:
正交投影又叫平行投影。投影视椎体是一个长方体,物体在投影平面的大小与距离远近没有关系。在OpenGL中我们可以通过 glm:ortho()这个函数来创建一个正交投影矩阵。正交投影其实是使用如下的 GL_PROJECTION矩阵进行变换。其中,变量r、l、t、b、n和f是视椎体的上下左右远近平面的边界变量。通过正交矩阵变换后,我们得到了裁剪空间。建筑蓝图绘制和计算机辅助设计需要使用到正交投影,因为这些行业要求投影后的物体尺寸及相互间的角度不变,以便施工或制造时物体比例大小正确。正交投影的示意图如前面右图所示。

透视投影:
根据我们的生活经验我们会发现这样的现象,离你越远的物体看起来越小,随着距离的增大,最终会消失在视野中,成为灭点。为了实现这种近大远小的效果,我们需要引入透视投影。在OpenGL中我们可以通过 glm:perspective() 这个函数来创建一个透视投影矩阵。投影变换使用的是齐次坐标,因为在透视除法阶段需要将XYZ的值除以W分量来获取NDC坐标空间。透视除法可以实现近大远小的视觉效果,该过程由硬件自动执行。这也是正交变换和透视变换最主要的区别,我们在后面会进行具体讨论。下图所示的矩阵是透视投影矩阵,和正交投影一样都是用来进行坐标空间变换的。

至于逐顶点着色,也叫高洛德着色(Gouraud Shading),得到的光照结果比较不自然,所以一般是在片元着色器中进行光照计算(使用Phong着色)。在此不作过多解释,后面集中阐述。
曲面细分着色器
这是一个可选的着色器,主要是对三角面进行细分,以此来增加物体表面的三角面的数量。借助它可以实现细节层次(LOD,Level-of-Detail)的机制,使得离摄像机越近的物体具有更加丰富的细节,而远离摄像机的物体具有较少的细节,如下图所示。
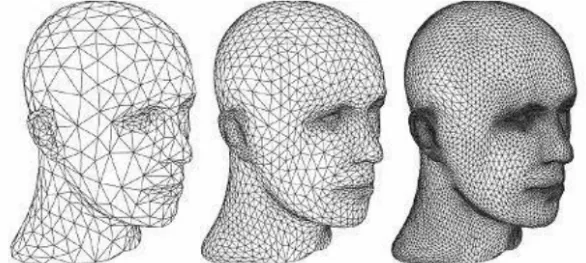
曲面细分是利用镶嵌化处理技术对三角面进行细分,以此来增加物体表面的三角面的数量,是渲染管线一个可选的阶段。它由**外壳着色器(Hull Shader)、镶嵌器(Tessellator)和域着色器(Domain Shader)**构成。
我们不创建**高模(high-poly)**来丰富网格信息主要是考虑到以下几个原因:
- 基于GPU可以实现动态的LOD技术,可以根据物体距离摄像机的远近来调整多边形网格的细节,比如说,若物体距离摄像机比较远,则按照高模的规格对它进行渲染会造成浪费,因为我们根本看不清网格的所有具体细节。随着物体和摄像机之间距离的拉近,我们可以实现连续镶嵌化处理,增加物体的细节。
- 节省内存。我们可以在各种存储器中保存低模网格信息,再根据需求用GPU动态地增加物体表面的细节。
几何着色器
几何着色器(Geometry Shader)也属于渲染管线的一个可选阶段,位于曲面细分(Tessellation)和光栅化(Rasterization)之间。顶点着色器以顶点数据作为输入数据,而几何着色器则以完整的图元(Primitive)作为输入数据。例如,以三角形的三个顶点作为输入,然后输出对应的图元。与顶点着色器不能销毁或创建顶点不同,几何着色器的主要亮点就是可以创建或销毁几何图元,此功能让GPU可以实现一些有趣的效果。例如,根据输入图元类型扩展为一个或更多其他类型的图元,或者不输出任何图元。需要注意的是,几何着色器的输出图元不一定和输入图元相同。几何着色器的一个拿手好戏就是将一个点扩展为一个四边形(即两个三角形)。
几何着色器输出的图元由顶点列表定义而成,而且顶点必须变换到裁剪空间。也就是说, 经过几何着色器处理后,得到的是一系列位于齐次裁剪空间的顶点所组成的图元。这些顶 点会在后面的裁剪、透视除法和光栅化阶段得到进一步处理。
几何着色器的一个主要的应用是显示物体的法线,这对于光照效果的调试非常有帮助。我们首先在不使用几何着色器的情况下正常渲染一次场景;然后开启几何着色器第二次渲染场景,送到几何着色器的是三角形图元,我们为其每个顶点生成一个法线向量。这样的效果类似于给表皮生成毛发,事实上,的确有比较老的游戏中,采用了此种方式生成密集的几何图形。

接下来我们看下几何着色器的另一个应用:动态几何体形成。我们利用几何着色器也可以实 现物体的LOD技术 (Level of Detail)。比如,我们需要在游戏中绘制一个圆圈,那么我们 可以根据距离摄像机的远近来调整圆圈的顶点数目,充分利用显卡的性能。
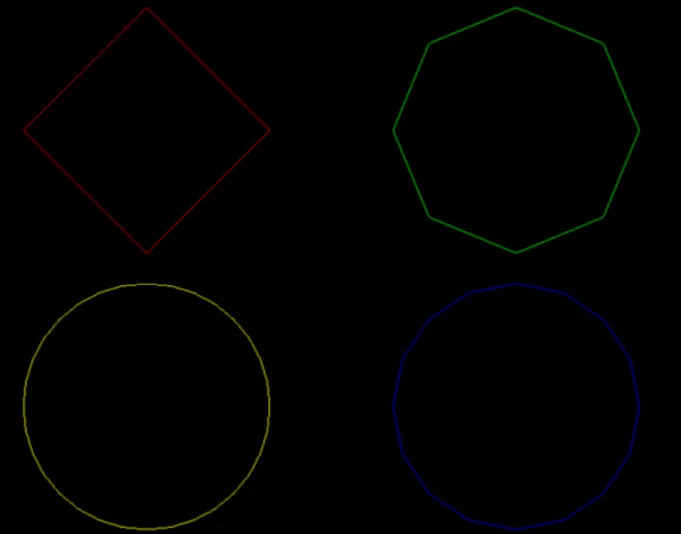
最后来说说最著名的BillBoard(告示牌)技术,公告牌技术就是以3D树木图片的四边形来代替3D树的渲染的技术。我们可以使公告牌总是面向摄像机,这样从远处看过去,公告牌不容易露出破绽,一个显著的应用就是《弹丸论破》的角色立绘。

图元组装(Primitive Assembly)
裁剪(Clipping)
经过顶点处理阶段,我们已经知道了顶点在裁剪空间的位置,接下来可以在裁剪空间中进行裁剪、背面剔除、屏幕映射等操作。
只有当图元部分或全部位于视椎体内时,我们才会将它送到流水线的下个阶段,也就是光栅化阶段。而完全位于视椎体外部的图元会被裁剪掉,不会对它们进行渲染。一些图元,它可能一部分位于摄像机视野内,另一部分在摄像机视野外部,外面这部分不需要进行渲染,可以将它裁剪掉。 例如,线段的两个顶点一个位于视椎体内而另一个位于视椎体外,那么位于外部的顶点将被裁剪掉,而且在视椎体与线段的交界处产生新的顶点来代替视野外部的顶点(在裁剪空间中进行)。
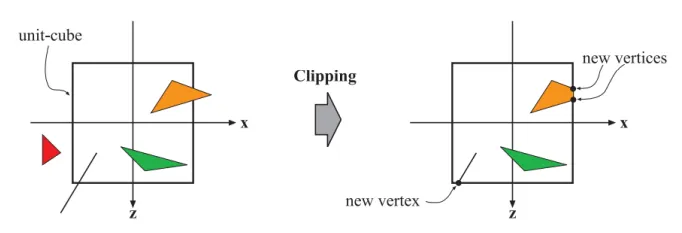
裁剪阶段使用的是4-分量的齐次坐标,在裁剪空间的基础上,进行 透视除法 (perspective division)后得到的坐标叫做归一化设备坐标(Normalized Device Coordinates,NDC),将坐标从裁剪空间的(-w,-w,w)变换为(-1,-1,1),即除 w,获得NDC坐标是为了实现屏幕坐标的转换与硬件无关。然后通过视口变换将NDC坐标变换到屏幕坐标,我们会在下面的屏幕映射具体讨论这两个部分。
不同图形API的NDC空间的z分量不同。在DirectX中,NDC空间的X和Y分量的范围是[-1, 1],而Z分量的范围是[0, 1]。而在OpenGL中,NDC空间的X、Y和Z分量的范围都是[-1, 1]。
常见的裁剪算法: ·Cohen-Sutherland算法 ·Liang-Barsky算法 ·Sutherland-Hodgman多边形裁剪算法
背面剔除(Back-Face Culling)
即背对摄像机的三角面剔除,上面我们讲到过模型数据中含有索引列表,列表中的三个点组成一个三角片,如果这三个点是顺时针排列的,认为是背面,否则认为是正面。
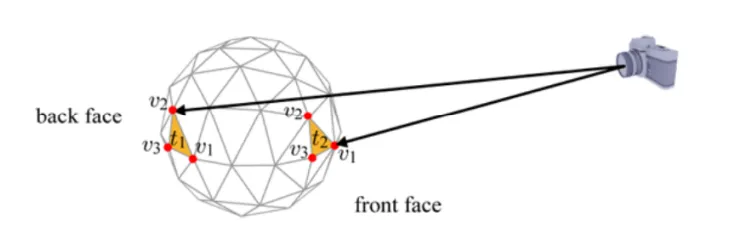
如下图所以,图元t1背向摄像机,需要被剔除,而图元t2需要被保留。我们利用三角形顶点的环绕顺序(Winding Order)来确定所谓的正面(front-face)和背面(back-face)。通常情况下,三角形的3个顶点是逆时针顺序(couter-clockwise,ccw)进行排列时,我们会认为是正面,而顺时针(clockwise,cw)排序时,我们会认为是背面。例如t2的三个顶点顺序为逆时针的(v1,v2,v3),所以是正面,需要保留。将t1和t2投影到XY平面后,我们可以清楚的看到它们顶点的环绕顺序。
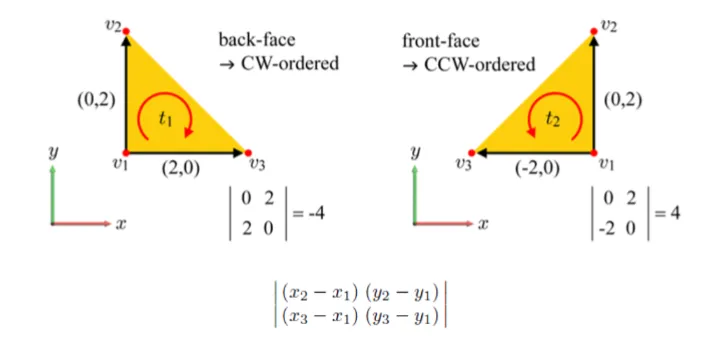
从上图可以看到,这里我们可以使用行列式(determinant)来确定投影后的2D三角形到底是CW还是CCW顺序。行列式的第一行由顶点v1和v2坐标确定,而第二行由顶点v1和v3坐标确定。如果行列式的值为负数,那么该三角面是背面朝向;如果为正数,则是正面朝向。
背面剔除的技术默认是不开启的。我们可以通过 glEnable(GL_CULL_FACE) 函数来开启背面剔除的优化。开启后,我们还可以通过glCullFace() 函数来配置剔除的是正面还是背面。参数为 GL_FRONT 、GL_BACK (默认值)和 GL_FRONT_AND_BACK 。
WARNING虽然背面剔除可以大概减少50%的渲染图元,但是在渲染半透明或不透明物体时,不能使用该技术,否则会出现穿帮的情况,因为半透明或不透明物体可以看到物体背后的东西。
屏幕映射(Screen Mapping)
**屏幕映射(ScreenMapping)**的任务是把每个图元的x和y坐标转换到屏幕坐标系(Screen Coordinates)下。屏幕坐标系是一个二维坐标系,它和我们用于显示画面的分辨率有很大关系。
从前面讨论的顶点变换我们知道:经过模型矩阵Model、观察矩阵View和投影矩阵Projection变换后,局部空间被变换到了裁剪空间(-Wc <= XYZ <= Wc)。
接下来,我们对向量除以w,进行齐次化的归一,我们可以得到标准设备空间,该空间一般也称作标准视体(Canonical View Volume,CVV)。这个行为我们称作透视除法 (Perspective Division)
执行透视除法是为了实现透射投影中近大远小的视觉效果,经过了投影矩阵Projection的变换后,W分量保留了观察空间中物体Z坐标的信息,所以透视除法才能够根据距离摄像机的远近正确实现透视效果。
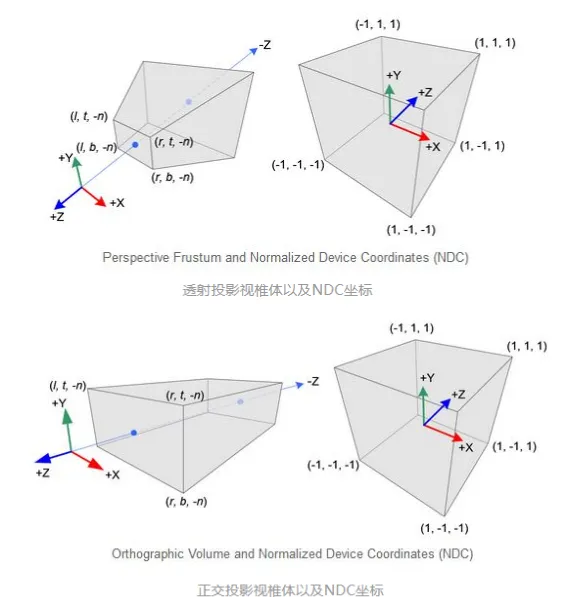
NOTE事实上,在硬件GPU层面上,透视除法在正交投影和透视投影中都会被执行,只不过正交投影变换并没有改变W分量的值(W分量的值仍是1),所以透视除法并没有实际的效果。我们从这里也明白了使用齐次坐标的意义,其实就是为了正确记录下投影变换前(观察空间)中物体的深度信息,也就是Z坐标的值。至于为什么要记录,敬请期待后面的深度测试部分吧~
最后为了转换到屏幕坐标空间,我们首先应用一下视口变换(Viewport Transform):
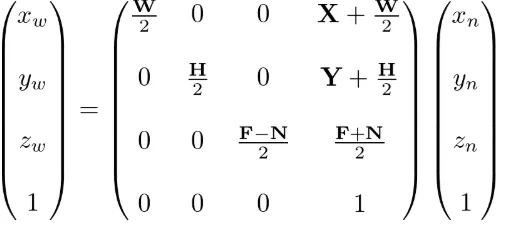
经过视口变换后,我们可以得到窗口坐标(Window Coordinates)。除了窗口坐标,还有屏幕坐标(Screen Coordinates)。一般来说,屏幕坐标是2D的概念,只用于表示屏幕XY坐标,而窗口坐标是2.5D的概念,它还带有深度信息,也就是经过变换后的Z轴的信息。 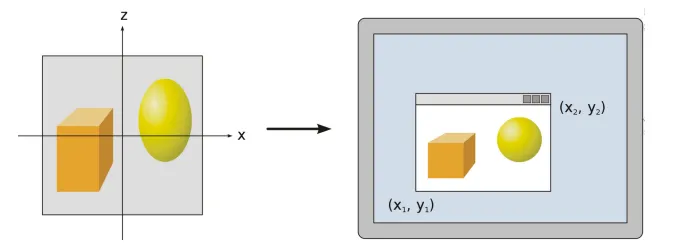
从上面视口变换的示意图我们注意到屏幕空间和Viewport其实是不一样的。在OpenGL中,我们可以通过 glViewport() 来设定视口的坐标和宽高。如果视口小于屏幕空间,那么会造成多余的像素被渲染。例如,glClear() 会为整个屏幕空间设定指定颜色值。我们可以通过裁切测试(Scissor Test)来指定渲染的区域,避免上面出现的渲染浪费的问题。我们会在后面的内容具体讨论裁切测试这种技术。
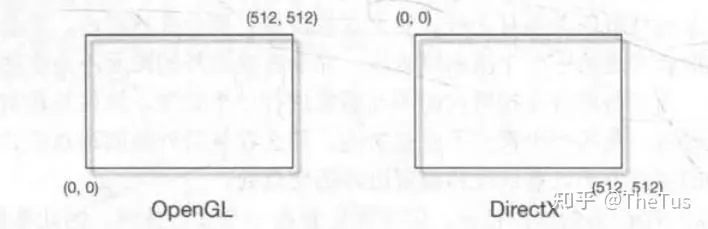
WARNING需要注意的是,不同图形API的屏幕坐标系也存在差异。 OpenGL把屏幕的左下角当成最小的窗口坐标值,而 DirectX 则定义了屏幕的左上角为最小的窗口坐标值。
总结
不知不觉光几何部分就写了不少了,光栅化和像素只能留到下次说了。。。